on
ComputerScience
Image Processing Convolution Kernels
As someone who’s relatively inexperienced with image processing, I started by looking at random image kernels on the web before applying it on the Matlab environment while I’m testing some random image kernels to see how all those image kernels perform against the test images. After that, I tweak the kernel’s values to see what will happen to the result with the new values.
For the example calculations and sample kernels used for this exploration purposes, I was using only 3x3 kernels.
Convolutional Transformation
Let’s suppose we have an image file with the dimension of 5x5 where the image is denoted as the input matrix \(A\). We’re aiming to transform the image using the 3x3 kernel \(K\). The definitions of \(A\) and \(K\) is as given below.
\[A = \left( \begin{matrix} 3 & 3 & 2 & 1 & 0 \\ 0 & 0 & 1 & 3 & 1 \\ 3 & 1 & 2 & 2 & 3 \\ 2 & 0 & 0 & 2 & 2 \\ 2 & 0 & 0 & 0 & 1 \\ \end{matrix} \right)\] \[K = \left( \begin{matrix} 0 & 1 & 2 \\ 2 & 2 & 0 \\ 0 & 1 & 2 \\ \end{matrix} \right)\]The \(A\) matrix will then be processed using the \(K\) matrix, resulting in an output matrix containing the output values of the convolution process. Below an animated illustration of the convolution process, which is taken from an article by Irhum Shafkat.
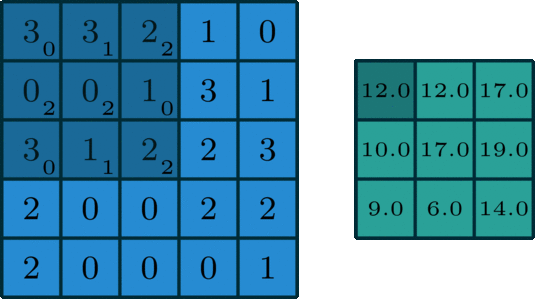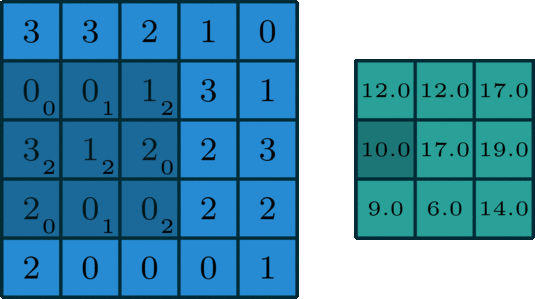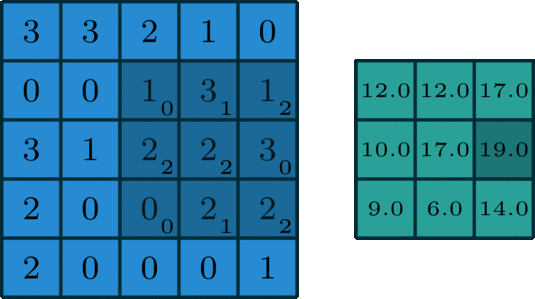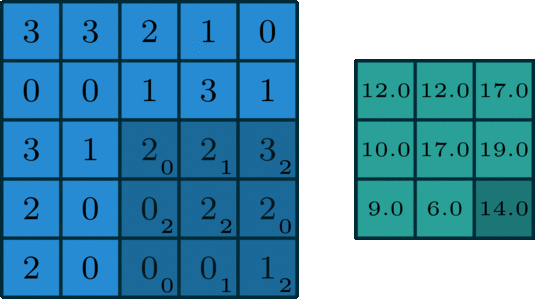
I defined the input matrix \(A\) with the same values as the input matrix in the illustration and the kernel matrix \(K\) also with the same values as in the kernel matrix in the illustration. Since we’re using the same matrices, I can take only a subset of the process to show how the calculation is done.
The following is the output matrix according to the illustration.
\[B = \left( \begin{matrix} 12.0 & 12.0 & 17.0 \\ 10.0 & 17.0 & 19.0 \\ 9.0 & 6.0 & 14.0 \\ \end{matrix} \right)\]Let’s take the top left value in the output matrix \(B\), which resulting value is 12.0. The value is generated from the processing of the 3x3 top left elements in the input matrix \(A\) transformed using kernel matrix \(K\).
\[mB_{1,1} = \left( \begin{matrix} 3 \times 0 & 3 \times 1 & 2 \times 2 \\ 0 \times 2 & 0 \times 2 & 1 \times 0 \\ 3 \times 0 & 1 \times 1 & 2 \times 2 \\ \end{matrix} \right) = \left( \begin{matrix} 0 & 3 & 4 \\ 0 & 0 & 0 \\ 0 & 1 & 4 \\ \end{matrix} \right)\]Then, we’re adding all of the elements in the resulting matrix together.
\[B_{1,1} = 0 + 3 + 4 + 0 + 0 + 0 + 0 + 1 + 4 = 12\]This process is basically two dot product operations.
\[mB_{1,1} = \left( \begin{matrix} 3 & 3 & 2 \\ 0 & 0 & 1 \\ 3 & 1 & 2 \\ \end{matrix} \right) \cdot \left( \begin{matrix} 0 & 1 & 2 \\ 2 & 2 & 0 \\ 0 & 1 & 2 \\ \end{matrix} \right) = \left( \begin{matrix} 0 & 4 & 8 \\ \end{matrix} \right)\] \[B_{1,1} = \left( \begin{matrix} 0 & 4 & 8 \\ \end{matrix} \right) \cdot \left( \begin{matrix} 1 \\ 1 \\ 1 \\ \end{matrix} \right) = 12\]This process is repeated until the all of the regions in the input matrix \(A\) is processed and the output is stored as an element in output matrix \(B\).
Example Kernels
During my search across the Internet, I stumbled upon this simple web-based demo of image kernels by Victor Powell on Setosa.io. He provides nine example kernels for us to test on sample images, one of them being an identity kernel.
All of the kernels provided by Victor Powell are 3x3 kernels, which is shown below. Some of the sample kernels below can be seen on Wikipedia’s list of kernels along with a sample result when the kernel is applied to an image.
Identity Kernel
\[K = \left( \begin{matrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{matrix} \right)\]The identity kernel wouldn’t cause any visible changes to the output image pixels if applied. As the name implies, this is akin to identity in mathematical operations where if an operation is performed between a number with its identity, it will result in the same number. Think \(1 + 0 = 1\) or \(1 \times 1 = 1\).
Blur
\[K = \left( \begin{matrix} 0.0625 & 0.125 & 0.0625 \\ 0.125 & 0.25 & 0.125 \\ 0.0625 & 0.125 & 0.0625 \\ \end{matrix} \right)\]This is a Gaussian blur kernel, to be exact. We can notice Gaussian kernels from the bell curve shaped by the values of the elements in the matrix if plotted. This kernel weights the elements closer to the center of the kernel during processing compared to those further from the center.
Blurring can be done to remove noise from images before applying edge detection.
Emboss
\[K = \left( \begin{matrix} -2 & -1 & 0 \\ -1 & 1 & 1 \\ 0 & 2 & 1 \\ \end{matrix} \right)\]Outline
\[K = \left( \begin{matrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{matrix} \right)\]Sharpen
\[K = \left( \begin{matrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \\ \end{matrix} \right)\]Edge Detection
While the previous filters are all named based on the expected visual effects on the image after the kernel is applied, the four Sobel kernels in the list aren’t. Sobel is a method for edge detection, for which Victor Powell provided four variations of the kernel on the demo. The top and bottom Sobel in the list are horizontal edge detectors, while the left and right Sobel are vertical edge detectors. For the complete edges to be formed, the result from the horizontal and vertical edge detectors need to be combined. It’s out of the coverage of this article.
There are a few other well-known edge detection methods, some of them are described briefly in this paper along with the result of the edge detection process on their sample images. In some cases, the outline kernel shown above is also considered as edge detection kernel (see edge detection kernel example on this Wikipedia page). Using the outline kernel for edge detection seems quite noisy though.
Top Sobel
\[K_{x} = \left( \begin{matrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \\ \end{matrix} \right)\]Bottom Sobel
\[K_{x} = \left( \begin{matrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \\ \end{matrix} \right)\]Left Sobel
\[K_{y} = \left( \begin{matrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \\ \end{matrix} \right)\]Right Sobel
\[K_{y} = \left( \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{matrix} \right)\]Experiment Tools
I’m using GNU Octave version 5.2.0 to help with the matrix operation calculations while also testing the kernels if applied to test images. GNU Octave is Matlab-compatible, so the code should be the same with Matlab.
The following is the sample code snippet for reading an image and applying filters to the image, also how to show the image.
pkg load image
A = imread('sample-image.jpg');
K = [-1, -2, -1; 0, 0, 0; 1, 2, 1]; % bottom Sobel kernel described above
B = imfilter(A, K);
imshow(A) % show original image
imshow(B) % show resulting image
References
Intuitively Understanding Convolutions for Deep Learning
Image Kernels Explained Visually
Study and Comparison of Different Edge Detectors for Image Segmentation